|
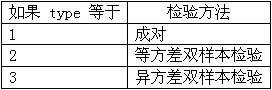
如果省略 known_x's,则假设该数组为 {1,2,3,...},其大小与 known_y's 相同。 New_x's 为需要函数 TREND 返回对应 y 值的新 x 值。 New_x's 与 known_x's 一样,每个独立变量必须为单独的一行(或一列)。因此,如果 known_y's 是单列的,known_x's 和 new_x's 应该有同样的列数。如果 known_y's 是单行的,known_x's 和 new_x's 应该有同样的行数。 如果省略 new_x's,将假设它和 known_x's 一样。 如果 known_x's 和 new_x's 都省略,将假设它们为数组 {1,2,3,...},大小与 known_y's 相同。 Const 为一逻辑值,用于指定是否将常量 b 强制设为 0。 如果 const 为 TRUE 或省略,b 将按正常计算。 如果 const 为 FALSE,b 将被设为 0(零),m 将被调整以使 y = mx。 72.返回数据集的内部平均值。函数 TRIMMEAN 先从数据集的头部和尾部除去一定百分比的数据点,然后再求平均值。当希望在分析中剔除一部分数据的计算时,可以使用此函数。 语法:TRIMMEAN(A,percent) A 为需要进行整理并求平均值的数组或数值区域。 Percent 为计算时所要除去的数据点的比例,例如,如果 percent = 0.2,在 20 个数据点的集合中,就要除去 4 个数据点 (20 x 0.2):头部除去 2 个,尾部除去 2 个。 73.返回与学生 t 检验相关的概率。可以使用函数 TTEST 判断两个样本是否可能来自两个具有相同平均值的总体。 语法:TTEST(A1,A2,tails,type) A1 为第一个数据集。 A2 为第二个数据集。 Tails 指示分布曲线的尾数。如果 tails = 1,函数 TTEST 使用单尾分布。如果 tails = 2,函数 TTEST 使用双尾分布。 Type 为 t 检验的类型。
74.计算基于给定样本的方差。 语法:VAR(N1,N2,...) N1,N2,... 为对应于总体样本的 1 到 30 个参数。 75.计算基于给定样本的方差。不仅数字,文本值和逻辑值(如 TRUE 和 FALSE)也将计算在内。 语法:VARA(V1,V2,...) V1,V2,... 对应于总体的一个样本的 1 到 30 个参数。 76.计算基于整个样本总体的方差。 语法:VARP(N1,N2,...) N1, N2, ... 为对应于样本总体的 1 到 30 个参数。 77.计算基于整个样本总体的方差。不仅数字,文本值和逻辑值(如 TRUE 和 FALSE)也将计算在内。 语法:VARPA(V1,V2,...) V1, V2,... 为对应于样本总体的 1 到 30 个参数。 78.返回韦伯分布。使用此函数可以进行可靠性分析,比如计算设备的平均故障时间。 语法:WEIBULL(x,alpha,beta,cumulative) X 参数值。 Alpha 分布参数。 Beta 分布参数。 Cumulative 指明函数的形式。 79.返回 z 检验的单尾概率值。对于给定的假设总体平均值 μ0,ZTEST 返回样本平均值大于数据集(数组)中观察平均值的概率,即观察样本平均值。 若要了解如何在公式中使用 ZTEST 计算双尾概率值的有关信息,请参阅下面的“说明”部分。 语法:ZTEST(A,μ0,sigma) A 为用来检验 μ0 的数组或数据区域。 μ0 为被检验的值。 Sigma 为样本总体(已知)的标准偏差,如果省略,则使用样本标准偏差。 |