|
这一文档适用于 "Gem for OneNote" Markdown 功能和 珍宝一脉"One Markdown" 套装。
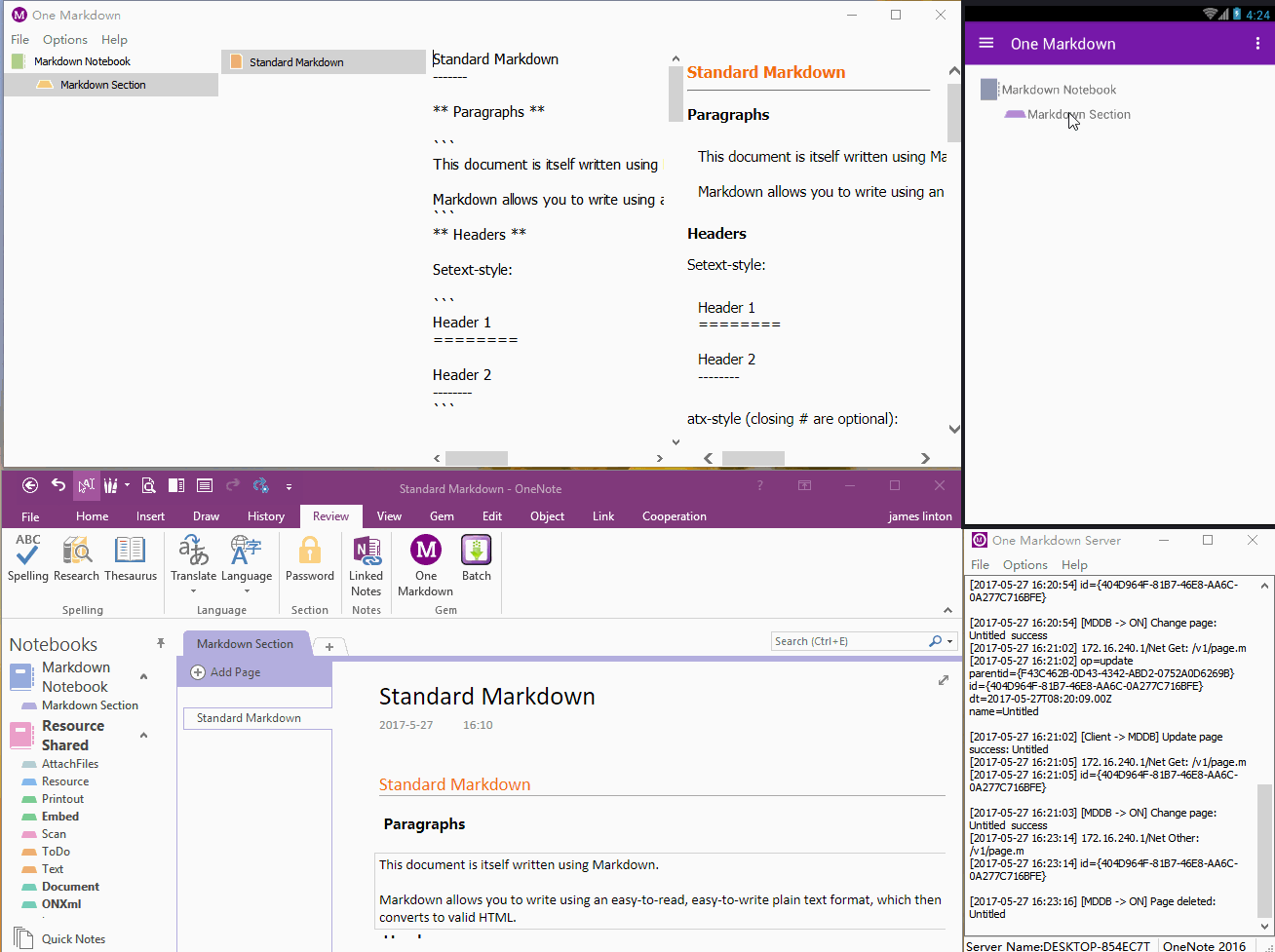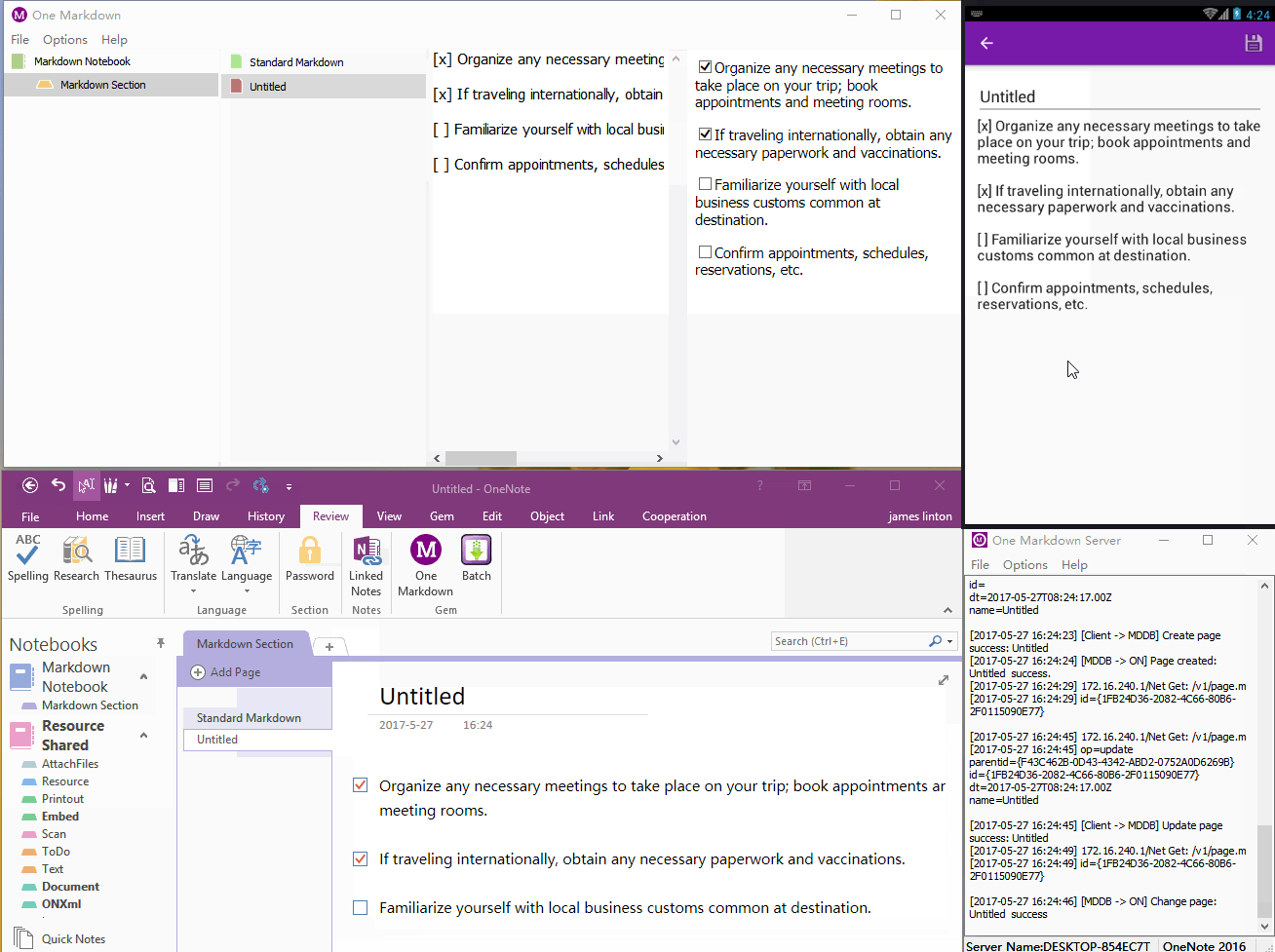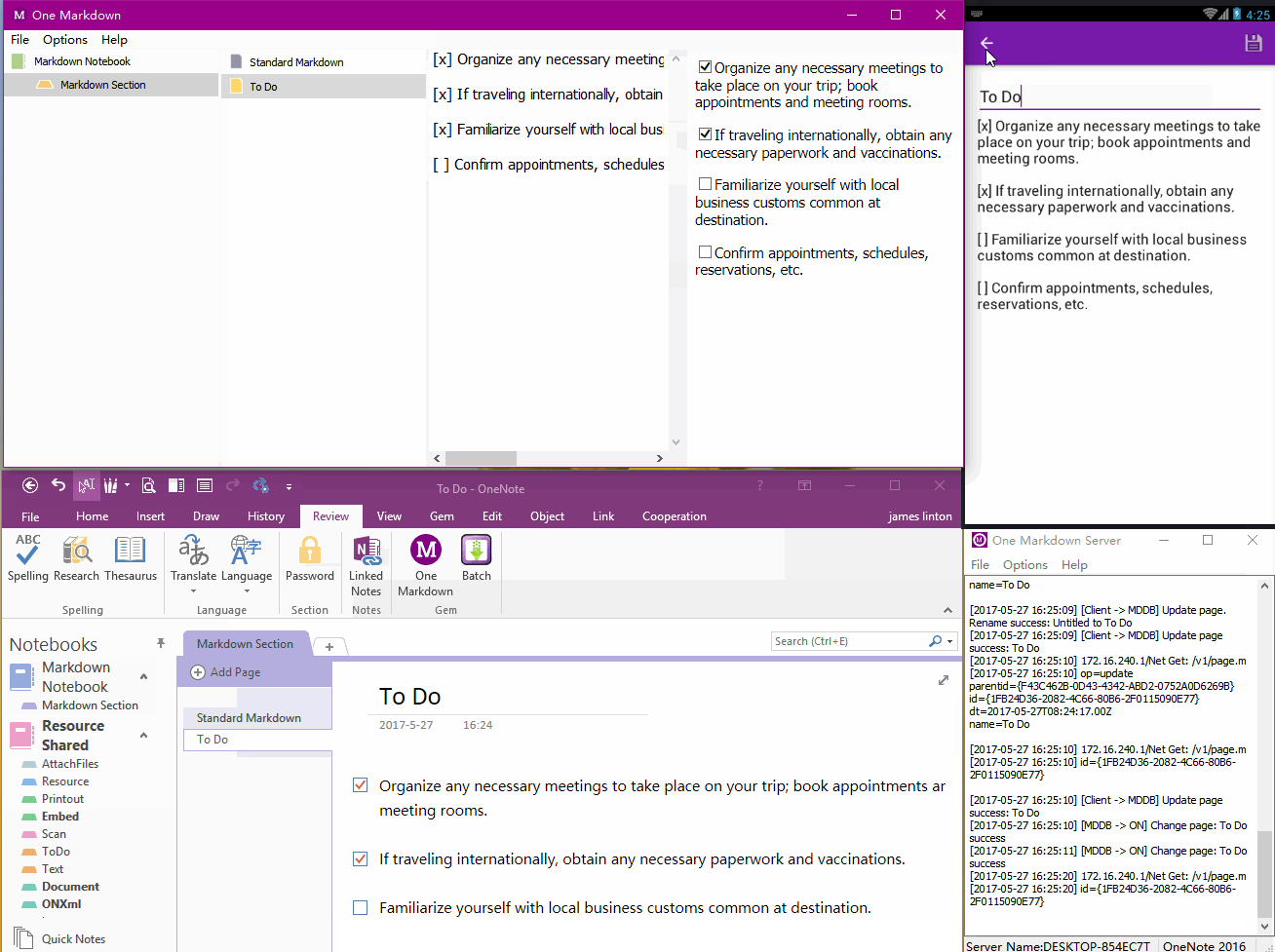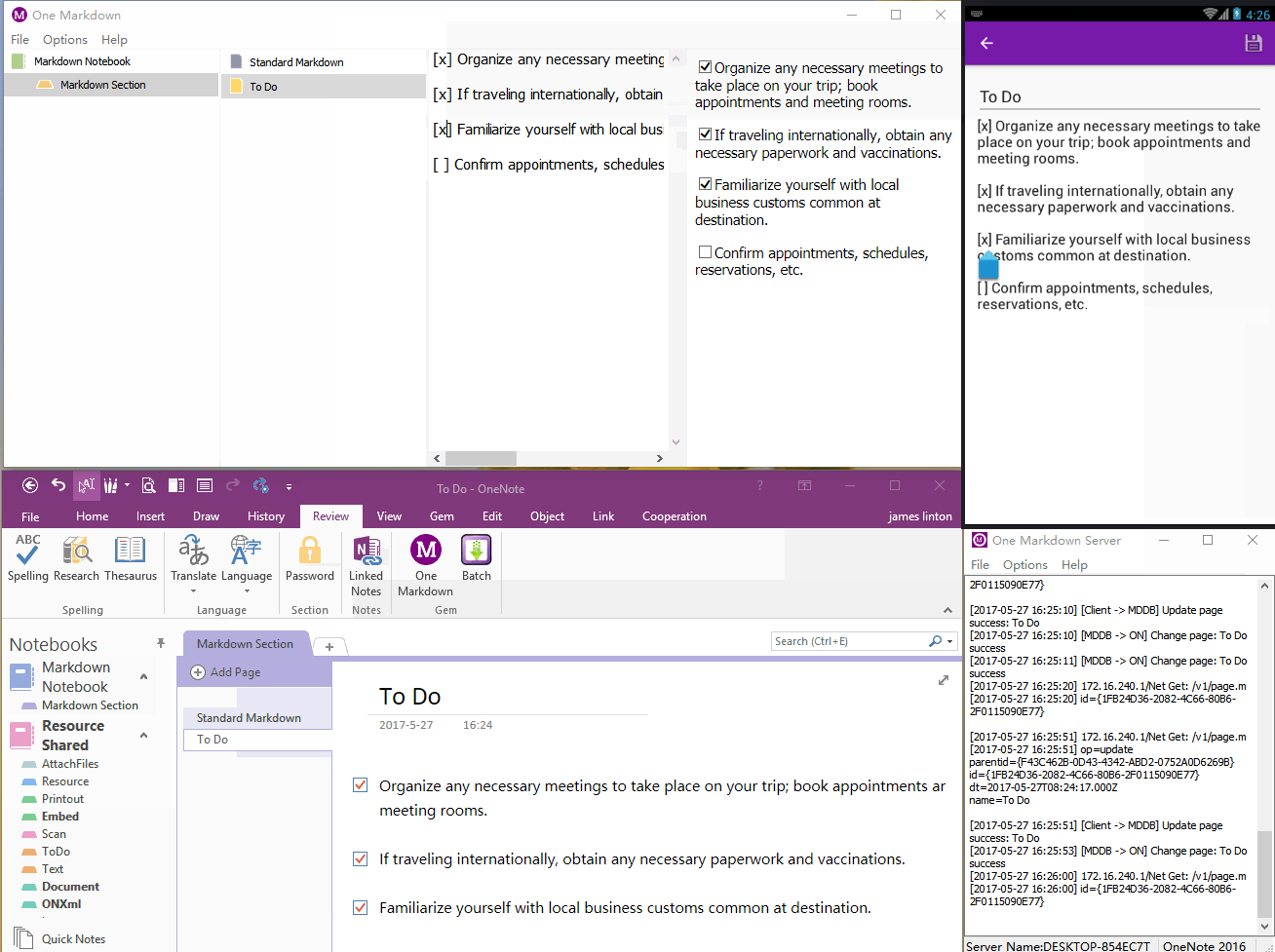
珍宝一脉 One Markdown
它通过局域网连接 OneNote 并进行笔记同步。实现在不通过 OneDrive 的情况下,同步 OneNote 笔记。
珍宝一脉 One Markdown for OneNote ( OneNote 内置编辑器 )
珍宝一脉 One Markdown (内置编辑器) 被包含在 Gem for OneNote 里,在安装完 Gem for OneNote 后,可以在 OneNote 的“审阅”选项卡下找到“珍宝一脉”功能。
这个编辑器可以让你直接在 OneNote 里编辑珍宝一脉的 Markdown 笔记。
Gem for OneNote 中使用 Markdown
- 首先在 OneNote 页面里输入 Markdown 文本。
- 然后点击“标记文本”功能,来转换 Markdown 文本为 OneNote 正常文本。
- 然后再点击一次“标记文本”功能,则把 OneNote 正常文本转换为 Markdown 文本。
标准 Markdown
文本块元素
标题
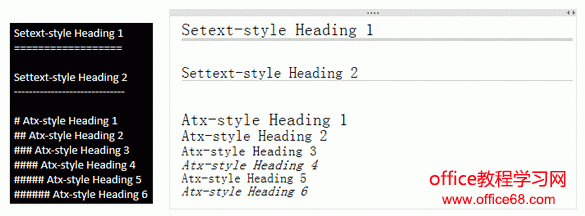
Markdown 支持 2 种类型的标题,Setext 和 atx 标题。
Setext 类型标题使用下划线的方式来定义。等号下划线为第一级标题,减号下划线为第二级标题。
Atx 类型标题,在行首插入 1 - 6 个井号 # 来对于 1- 6 种标题。
列表
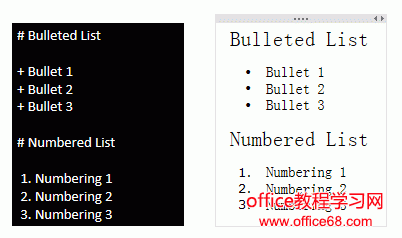
Markdown 支持有序列表(编号列表)和无序列表(项目符号列表)。
无序列表可以使用星号 *,加号 +,减号 - 作为列表标记。
有序列表则使用数字和一个英文句点作为列表标记。
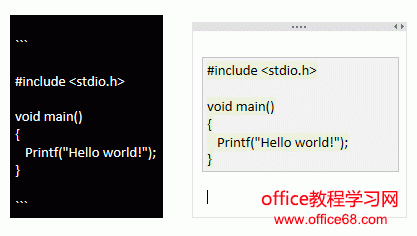
代码块
可以使用 3 个反引号 ``` 或者 3 个上飘号 ~~~ 把程序代码括起来。
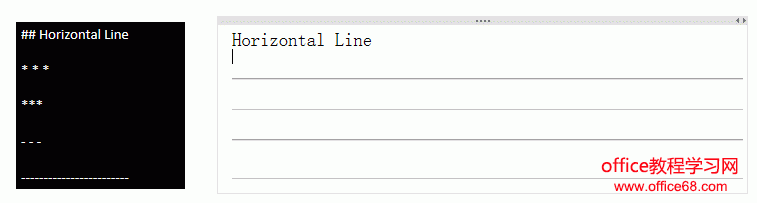
水平线
使用 3 个星号 ***,或者 3 个减号 ----, 或者 3 个下划线 ___ 来建立水平线。
小块元素
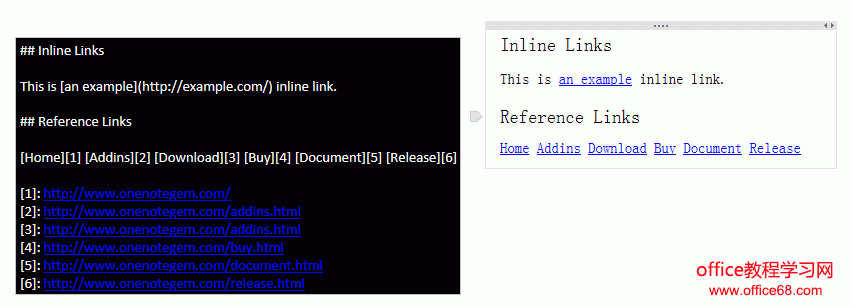
链接
Markdown 支持 2 中链接:行内链接和引用链接。
这两种形式的链接都是使用方括号 [ 链接 ] 来进行标记。
斜体和粗体
Markdown 使用星号* 或者是下划线 _ 作为斜体标记,双星号 ** 或者双下划线 __ 作为粗体标志。
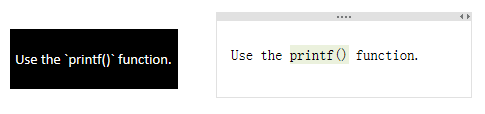
行内小代码块
在行内,可以使用单反引号 ` 括起小代码块。
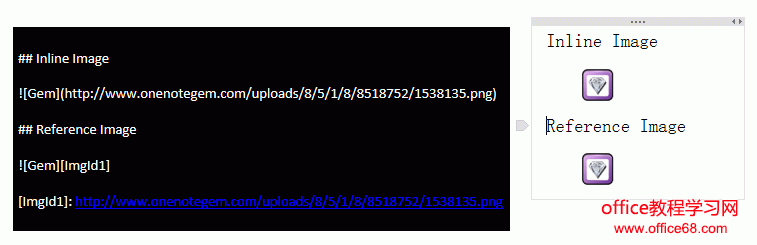
图片
Markdown 可以使用 2 种方式来引用图片:行内图片形式和引用形式。
转义符
以下字符需要使用反斜杠 \ 来进行转移:
\ 反斜杠
` 反引号
* 星号
_ 下划线
{} 花括号
[] 方括号
() 圆括号
# 井号
+ 加号
- 减号
. 圆点
! 感叹号
扩展元素
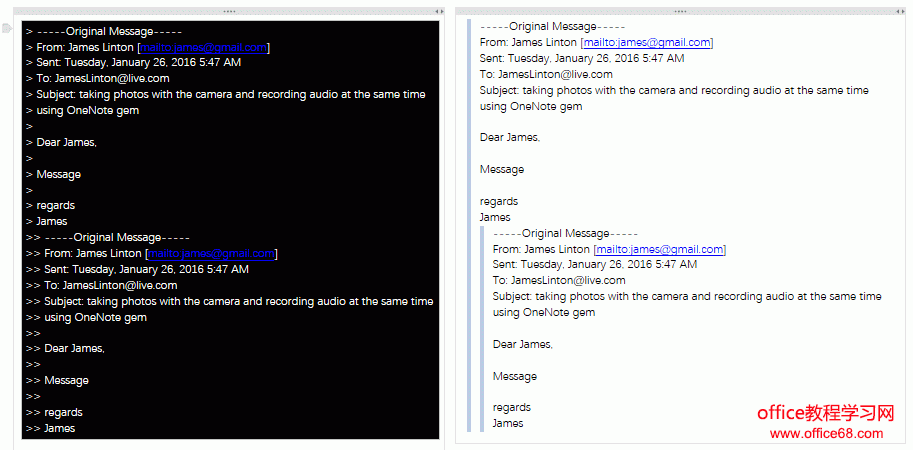
文本缩进
使用多个尖括号对文本进行多层缩进 ">", ">>", ">>>" ...
珍宝一脉 One Markdown 的扩展元素
目录大纲(详细)
标题目录。
[TOC]
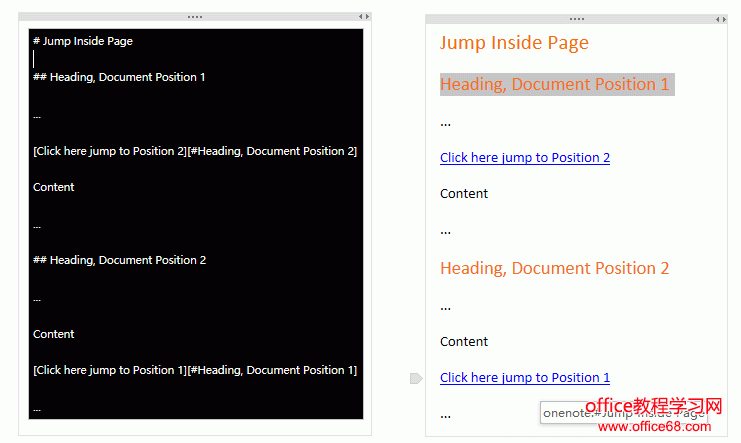
标题类型引用链接 - 页内跳转链接 (详细)
使用引用标题文字来制作页面链接,实现在页面内进行跳转。
格式:[显示文字][#标题文字]
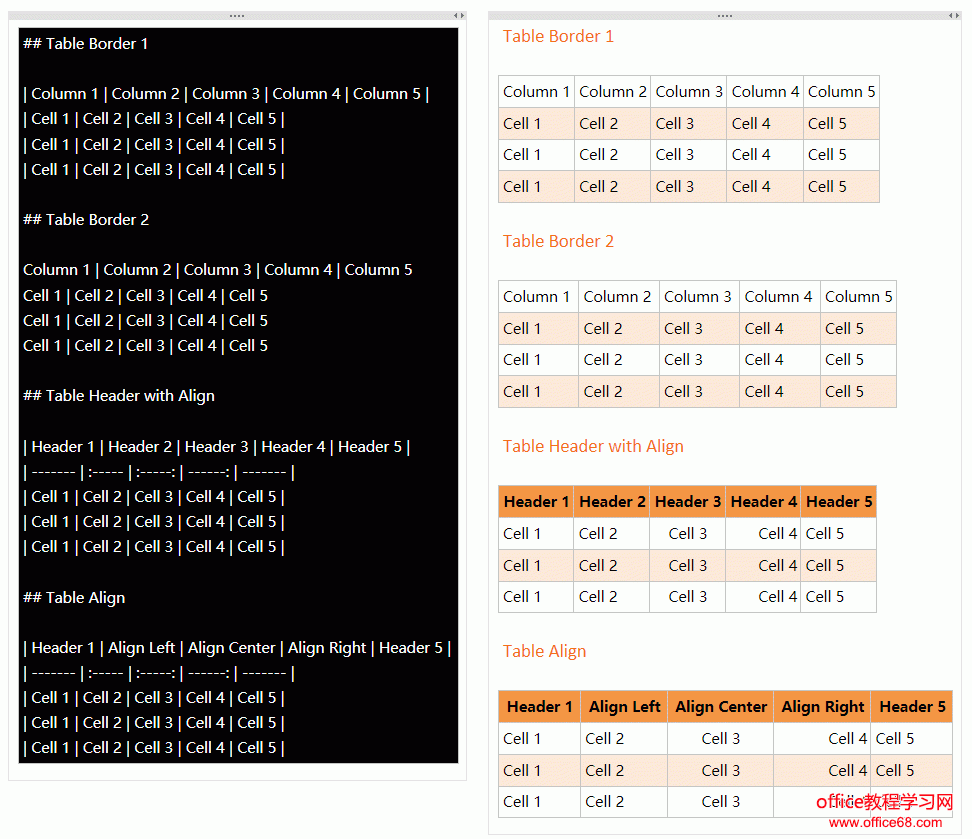
表格
使用竖线 | 来划分表格的列。
可选,第二行作为表头划分。
--- 或者 :--- 表示文字靠左排列
:--: 表示文字居中
--: 表示文字靠右排列
| Header 1 | Header 2 | Header 3 | Header 4 | Header 5 |
| ----------- | :----------- | :----------: | -----------: | ------------ |
| Cell 1 | Cell 2 | Cell 3 | Cell 4 | Cell 5 |
| Cell 1 | Cell 2 | Cell 3 | Cell 4 | Cell 5 |
| Cell 1 | Cell 2 | Cell 3 | Cell 4 | Cell 5 |
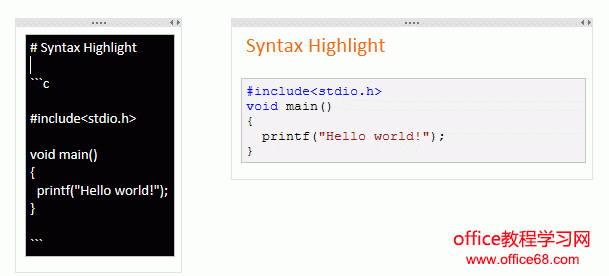
计算机语言语法高亮(详细)
计算机高亮语言支持:bash, c, cpp, csharp, css, pas, java, js, perl, pl, php
```c
#include<stdio.h>
void main()
{
printf("Hello world!");
}
```
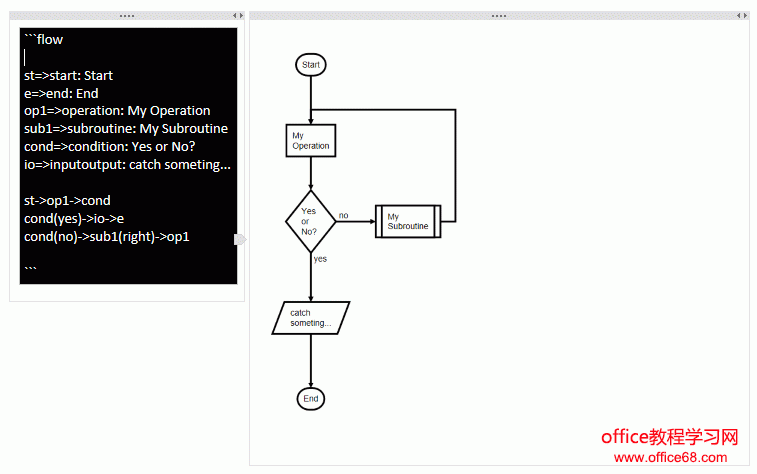
流程图(详细)
# 流程图 1
```flow
st=>start: Start
e=>end: End
op1=>operation: My Operation
sub1=>subroutine: My Subroutine
cond=>condition: Yes or No?
io=>inputoutput: catch someting...
st->op1->cond
cond(yes)->io->e
cond(no)->sub1(right)->op1
```
|
# 流程图 2
```flow
st=>start: Start|past:>http://www.google.com[blank]
e=>end: End:>http://www.google.com
op1=>operation: My Operation|past
op2=>operation: Stuff|current
sub1=>subroutine: My Subroutine|invalid
cond=>condition: Yes
or No?|approved:>http://www.google.com
c2=>condition: Good idea|rejected
io=>inputoutput: catch something...|request
st->op1(right)->cond
cond(yes, right)->c2
cond(no)->sub1(left)->op1
c2(yes)->io->e
c2(no)->op2->est=>start: Start|past:>http://www.google.com[blank]
e=>end: End:>http://www.google.com
op1=>operation: My Operation|past
op2=>operation: Stuff|current
sub1=>subroutine: My Subroutine|invalid
cond=>condition: Yes
or No?|approved:>http://www.google.com
c2=>condition: Good idea|rejected
io=>inputoutput: catch something...|request
st->op1(right)->cond
cond(yes, right)->c2
cond(no)->sub1(left)->op1
c2(yes)->io->e
c2(no)->op2->e
```
|
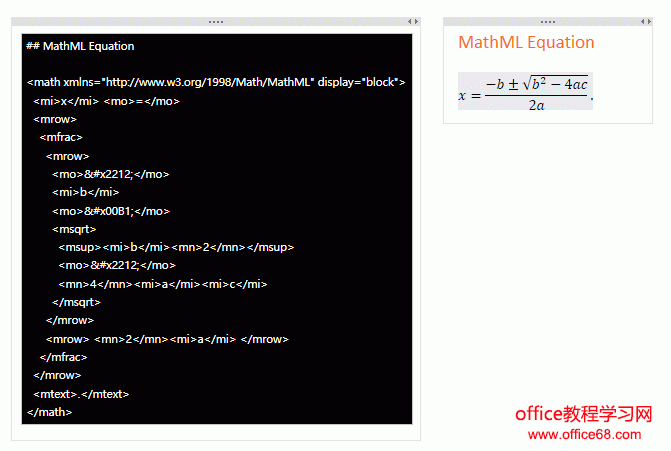
MathML 公式(详细)
MathML 使用 <math> 和 </math>标签对 XML 文本进行封装。
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mi>x</mi> <mo>=</mo>
<mrow>
<mfrac>
<mrow>
<mo>−</mo>
<mi>b</mi>
<mo>±</mo>
<msqrt>
<msup><mi>b</mi><mn>2</mn></msup>
<mo>−</mo>
<mn>4</mn><mi>a</mi><mi>c</mi>
</msqrt>
</mrow>
<mrow> <mn>2</mn><mi>a</mi> </mrow>
</mfrac>
</mrow>
<mtext>.</mtext>
</math>
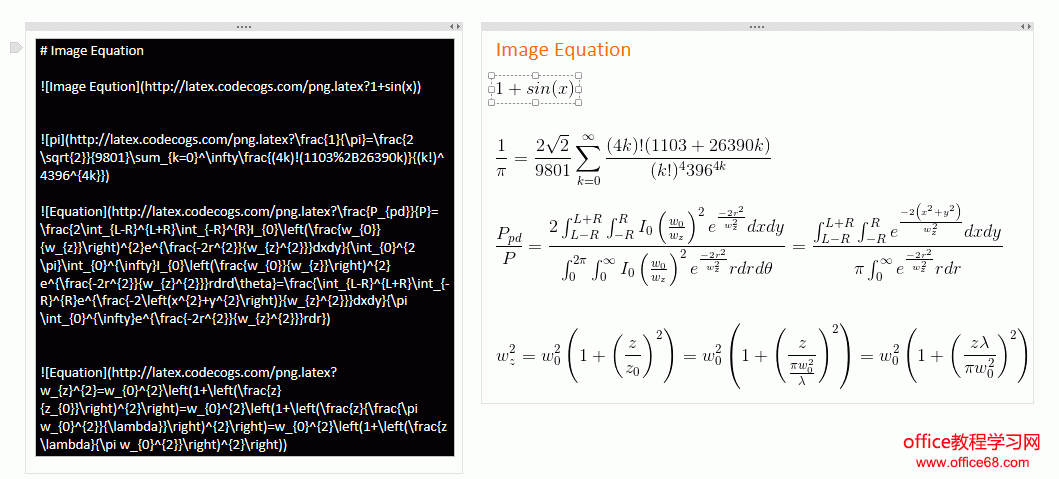
图片类 LaTeX 公式 (详细)
# Image Equation
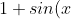)
!(1103%2B26390k)}{(k!)^4396^{4k}})
^{2}e^{\frac{-2r^{2}}{w_{z}^{2}}}dxdy}{\int_{0}^{2\pi}\int_{0}^{\infty}I_{0}\left(\frac{w_{0}}{w_{z}}\right)^{2}e^{\frac{-2r^{2}}{w_{z}^{2}}}rdrd\theta}=\frac{\int_{L-R}^{L+R}\int_{-R}^{R}e^{\frac{-2\left(x^{2}+y^{2}\right)}{w_{z}^{2}}}dxdy}{\pi\int_{0}^{\infty}e^{\frac{-2r^{2}}{w_{z}^{2}}}rdr})
^{2}\right)=w_{0}^{2}\left(1+\left(\frac{z}{\frac{\pi w_{0}^{2}}{\lambda}}\right)^{2}\right)=w_{0}^{2}\left(1+\left(\frac{z\lambda}{\pi w_{0}^{2}}\right)^{2}\right))
|