|
随着云计算应用的广泛普及,云计算与互联网的结合也日益紧密,以IPv6为代表的下一代互联网将是未来云计算最优化的选择方案之一。IPv6协议是下一代互联网的核心网络协议,能够更加有效地为云平台及云应用提供网络资源保障和强有力的技术支撑。目前,云用户在享受云计算带来的极大便利的同时,也面临着一些问题,其中重要的问题之一是资源分配问题。为了能够高效地管理资源,实现资源利用率最大化,在云平台资源管理中引入预测技术[1],根据负载情况有效的预测资源使用量,进行合理的资源调度,避免不必要的虚拟机迁移。资源预测技术是优化云计算资源分配的非常有效的方法[2]。 目前资源预测方法较多,对云资源预测的研究大致可以分为两类。第一类预测方法采用经典模型,包括时间序列模型、神经网络模型、支持向量机、马尔科夫模型、贝叶斯模型等。文献[3]利用线性预测方法,如指数移动平均线、二阶自回归移动平均线和移动平均法,预测时间序列数据的工作量。文献[4]为SaaS供应商提供了一个基于自回归移动平均模型(ARIMA)的云工作负载预测模块,提出基于ARIMA模型的预测并使用真实的Web服务器请求数据来评估预测未来工作负载的准确性,此外还评估了预测准确性对资源利用和QoS效率等方面的影响文献[5]利用支持向量机(SVMs)方法的时间序列预测时间序列数据,用于响应时间和吞吐量。文献[6]提出了一种贝叶斯模型,通过在几个数据中心的工作负载模式基础上考虑几个参数,以预测短期和长期的虚拟资源需求。文献[7]分析了云计算的工作负载,并进一步评估了Markov建模和贝叶斯建模等两种预测技术的性能。第二类是针对特定的云工作负载模式进行预测。云环境下现有资源预测模型通常采用单一的预测策略,忽略了其他因素对网络资源的内在作用,导致数据隐含信息丢失量大,所以往往难以取得准确的预测结果的问题。 同时,资源类型的异质性和应用的资源需求变化对云中的工作量预测造成了新的挑战。 针对这一问题,本文提出一种基于ARIMA-Kalman混合模型预测方法。该方法将卡尔曼滤波与自回归积分滑动平均模型相结合,对工作负载所需的资源进行预测。实验结果表明,与单一模型的预测方法相比,该方法具有更高的预测精度,有效的提高了资源利用率,能够很好为虚拟机资源的按需调度提供帮助。 1.预测模型理论 1.1 ARIMA模型 自回归积分滑动平均模型(ARIMA)[8]属于时间序列预测方法,ARIMA模型对采集到的工作负载执行的历史信息进行拟合,由此预测一个负载在未来的执行时间。ARIMA(p , d , q)模型可以表示为:
其中P为自回归阶数,d为差分次数,q为移动平均阶数,为原序列;为白噪声序列,其均值为0;B为后移算子;为自回归算子,为移动算子;为参数, 该方法主要分为四个步骤: 第一步,首先确定是否为平稳序列。对于非平稳序列,作差分转换为平稳序列,实现ARIMA模型向ARMA模型的转换。然后,通过序列的自相关系数(AC)和偏自相关系数(PAC)来确定识别AR/MA[9]。 第二步,确定ARIMA模型中的参数。通过穷举参数值对数据进行拟合,评定拟合结果的标准一般是将原序列和拟合的结果序列作差构成残差序列,同时通过比较残差序列的纯随机性来比较拟合程度的好坏[9]。 第三步,将确定的模型对历史数据进行拟合,同时检验拟合的效果。 第四步,使用经过检验的模型,通过对工作负载执行的历史信息进行数据分析,预测未来的负载。 基于ARIMA模型的预测公式如下所示:
其中,z(t+1),z(t),…z(t-p+1)为t+1,t,…,t-p+1时刻对应的工作负载资源利用率的值; ARIMA建模优点在于不需要太多的样本序列就可以建立预测模型,但具有低阶ARIMA模型预测精度不高、高阶模型参数不易估计的缺点[10]。 1.2 Kalman滤波模型 卡尔曼滤波(Kalman)是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法[11]。 Kalman滤波一般步骤如下: 首先要引入一个线性随机微分方程来表示系统状态: 再加上系统的测量值: 其中, 假设现在的系统状态是K,则可以通过系统的前一状态进行预测得出当前状态,如公式(5)所示: 系统的预测结果已经更新了,则对应的 式(6)中, 结合预测值和测量值,可以得到现在状态的最优化估算值 其中 通过更新K状态下 其中 卡尔曼滤波预测算法有很多优点。它只依赖于递归方法,不需要所有的历史数据。它不仅可以用来处理静止和非平稳的随机过程,还可以用来处理时变和非时变的系统。 2.基于ARIMA-Kalman的工作负载资源预测模型 鉴于以上资源预测方法中,ARIMA模型虽然能较好地实现工作负载的资源预测,但是存在低阶预测精度较低,高阶参数估困难的问题。卡尔曼滤波模型虽然可以动态修改预测权值,通过递推方程实现较高的预测精确度,但是基于卡尔曼滤波的工作负载的资源预测的状态方程和测量方程难以得到。所以本文提出了一种组合算法,首先利用ARIMA模型建立一个能反映负载时间序列数据变化规律的低阶模型,然后将Kalman滤波模型的预测方程与其结合,推导出其状态方程和测量方程,利用卡尔曼预测迭代方程以实现工作负载资源的预测。 一般来说,卡尔曼滤波的观测方程和测量方程可以分别描述为公式(10)(11):
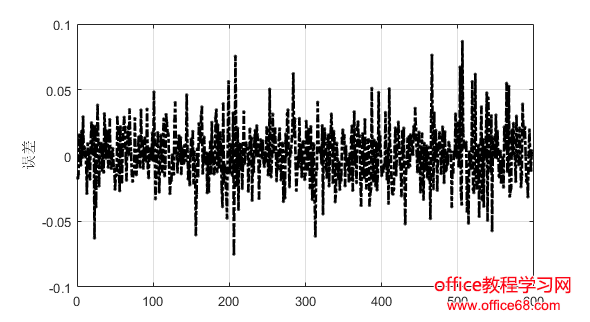
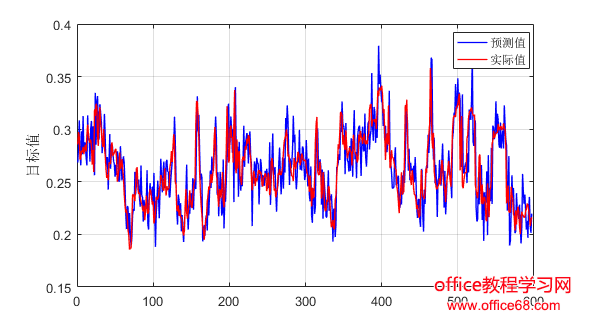
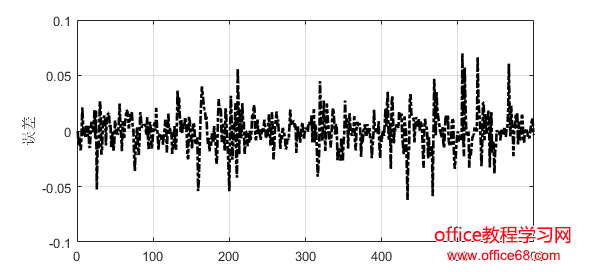
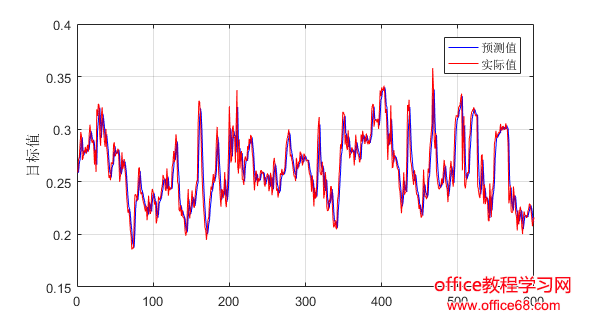
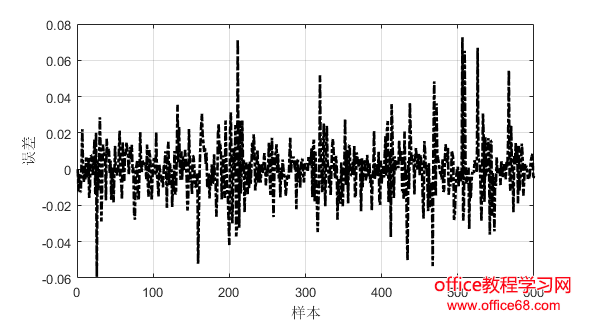
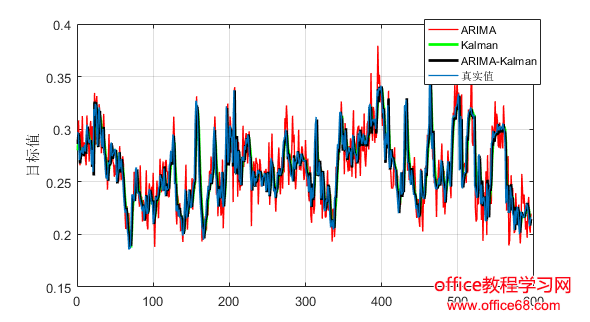
3.实验分析 3.1实验数据 为了评估所提出的方法,我们使用了来自谷歌数据中心于2011年公布的实际负载跟踪进行了实验[12]。公布的数据包括29天的跟踪日志,提供了CPU、内存和磁盘的利用率。本文我们只考虑CPU利用率。Google数据集中的CPU使用信息是粗粒度的,每300秒记录一次。 由于谷歌数据集数据量很大,处理起来非常费时间。本文采用AWK处理日志文件,提取合并过滤数据,生成CSV文件,再读入Matlab来处理的。本文采用均方根误差RMSE、平均绝对误差MAE、均方误差MSE作为指标来评估模型的表现。 3.2实验结果 将数据进行处理之后得到8352个样本,我们将前7752个样本数据用来训练,最后600个样本用来预测。首选用ARIMA模型进行预测,预测结果和误差如图1和图2所示。随后用Kalman滤波模型进行预测,预测结果和误差如图3和图4所示。最后用ARIMA-Kalman模型进行预测,预测结果和误差如图5和图6所示。通过观察图1、图3和图5,ARIMA模型预测结果的误差波动较大且不稳定,Kalman滤波预测结果误差次之,ARIMA-Kalman混合模型的误差最稳定且总体趋势趋近于0。 图1 ARIMA模型预测误差图 图2 ARIMA模型预测结果图
图3 Kalman滤波模型预测误差图
图4 Kalman滤波模型预测结果图
图5 ARIMA-Kalman模型预测误差图
图6 ARIMA-Kalman模型与其他模型对比图
表1 各模型评价指标对比
表1显示各模型预测结果的RMSE、MAE、MSE。方根误差(RMSE)对一组测量中的特大或特小误差反映非常敏感,所能够很好地反映出测量的精密度。ARIMA模型、Kalman滤波、ARIMA-Kalman混合模型的RMSE依次为0.0214、0.0158、0.0147,则可以说明ARIMA-Kalman混合模型的预测精度最高。平均绝对误差由于离差被绝对值化,不会出现正负相抵消的情况,因而,平均绝对误差能更好地反映预测值误差的实际情况。ARIMA模型、Kalman滤波、ARIMA-Kalman混合模型的MAE分别为0.0169、0.01143、0.01009,所以通过误差图和MAE值更能够说明混合模型误差低于单一模型。 所以通过以上信息对比很明显发现ARIMA-Kalman预测精度要高于其他单一模型的预测精度,有效的提高了资源利用率,为虚拟机资源的按需调度提供帮助。 4.结论 网络负载资源预测可以减少云数据中心的过量资源消耗,是有效的管理资源的一种重要方法。工作负载预测的其他主要好处包括有效的资源利用率、有效的资源可伸缩性、避免工作负载处理失败、容量规划、网络分配、任务调度、负载平衡、性能优化和维护预先确定的QoS和SLA(服务级别协议)等。但是目前多数研究主要集中运于用单一的模型对网络负载进行预测,预测精度往往达不到预期。 考虑到这一点,本文研究的目的在于分析云的工作负载,并进一步提出一种混合预测模型,充分利用了ARIMA模型和Kalma滤波模型的优点,通过ARIMA模型建立一个能反映负载时间序列数据变化规律的低阶模型,然后将Kalman滤波模型的预测方程与其结合,利用卡尔曼预测迭代方程以实现工作负载资源的预测。并通过Google数据集进行验证表明该混合模型预测精度比其他单一模型提高很多,有效的提高了资源利用率和虚拟机资源的按需调度的效率,这将为改进整个云系统的性能带来广泛的有益的贡献。 参考文献 [1]张飞飞, 吴杰, 吕智慧. 云计算资源管理中的预测模型综述[J]. 计算机工程与设计, 2013, 34(9): 3078-3083. [2]刘晓艳, 王颖. 基于改进云模型的云计算负载预测[J]. 计算机应用研究, 2015, 32(10):3124-3127. [3]Roy N, Dubey A, Gokhale A. Efficient autoscaling in the cloud using predictive models for workload forecasting[C]//Cloud Computing (CLOUD), 2011 IEEE International Conference on. IEEE, 2011: 500-507. [4]Calheiros R N, Masoumi E, Ranjan R, et al. Workload prediction using ARIMA model and its impact on cloud applications’ QoS[J]. IEEE Transactions on Cloud Computing, 2015, 3(4): 449-458. [5]Sapankevych N I, Sankar R. Time series prediction using support vector machines: a survey[J]. IEEE Computational Intelligence Magazine, 2009, 4(2). [6]Shyam G K, Manvi S S. Virtual resource prediction in cloud environment: A Bayesian approach[J]. Journal of Network and Computer Applications, 2016, 65: 144-154. [7]Panneerselvam J, Liu L, Antonopoulos N, et al. Workload analysis for the scope of user demand prediction model evaluations in cloud environments[C]//Proceedings of the 2014 IEEE/ACM 7th International Conference on Utility and Cloud Computing. IEEE Computer Society, 2014: 883-889. [8]刘峰, 王儒敬, 李传席. ARIMA模型在农产品价格预测中的应用[J]. 计算机工程与应用, 2009, 45(25):238-239. [9]华哲邦, 李萌, 赵俊峰,等. 基于时间序列分析的Web Service QoS预测方法[J]. 计算机科学与探索, 2013, 7(3):218-226. [10]张韬, 张兴裕, 刘元元, 等. 基于 ARIMA 模型的 Kalman 滤波算法在淋病发病率预测的应用初探[J]. 现代预防医学, 2013, 16: 005. [11]李明干. 短期负荷预测的卡尔曼滤波神经网络算法研究[D]. 华中科技大学, 2004. [12]Reiss C, Wilkes J, Hellerstein J L. Google cluster-usage traces: format+ schema[J]. Google Inc., White Paper, 2011: 1-14. [13]Xu D, Wang Y, Jia L, et al. Real-time road traffic state prediction based on ARIMA and Kalman filter[J]. Frontiers of Information Technology & Electronic Engineering, 2017, 18(2): 287-302. [14]Emeakaroha V C, Brandic I, Maurer M, et al. SLA-aware application deployment and resource allocation in clouds[C]//Computer Software and Applications Conference Workshops (COMPSACW), 2011 IEEE 35th Annual. IEEE, 2011: 298-303. [15]Gong Z, Gu X, Wilkes J. Press: Predictive elastic resource scaling for cloud systems[C]//Network and Service Management (CNSM), 2010 International Conference on. IEEE, 2010: 9-16. [16]Ghorbani M, Wang Y, Xue Y, et al. Prediction and control of bursty cloud workloads: a fractal framework[C]//Proceedings of the 2014 International Conference on Hardware/Software Codesign and System Synthesis. ACM, 2014: 12. [17]Chen B S, Peng S C, Wang K C. Traffic modeling, prediction, and congestion control for high-speed networks: a fuzzy AR approach[J]. IEEE Transactions on Fuzzy Systems, 2000, 8(5): 491-508. [18]MA J, YANG H. Application of adaptive kalman filter in power system short-term load forecasting [J]. Power System Technology, 2005, 29(1):75-79. [19]Taylor J W, De Menezes L M, McSharry P E. A comparison of univariate methods for forecasting electricity demand up to a day ahead[J]. International Journal of Forecasting, 2006, 22(1): 1-1 |
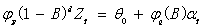
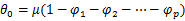 ,为平均数[9]。
,为平均数[9]。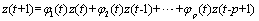
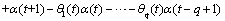 (2)
(2)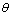 和
和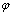 分别代表t时刻的滑动平均项系数和自回归项系数。
分别代表t时刻的滑动平均项系数和自回归项系数。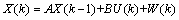 (3)
(3)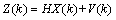 (4)
(4) 和
和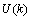 分别表示是
分别表示是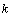 时刻的系统状态和对系统的控制量。
时刻的系统状态和对系统的控制量。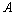 和
和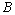 表示系统参数。
表示系统参数。 和
和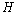 分别表示系统在时刻的测量值和测量系统的参数。
分别表示系统在时刻的测量值和测量系统的参数。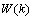 和
和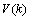 分别表示系统过程和测量的高斯白噪声,其协方差分别是
分别表示系统过程和测量的高斯白噪声,其协方差分别是 和
和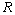 。
。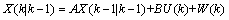 (5)其中,
(5)其中,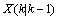 是对当前状态的预测值,
是对当前状态的预测值,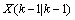 是前一状态最优解,
是前一状态最优解,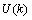 为现在状态的控制量。
为现在状态的控制量。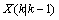 的协方差同时进行更新。我们用
的协方差同时进行更新。我们用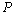 表示
表示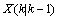 的协方差:
的协方差: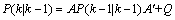 (6)
(6)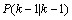 是
是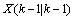 的协方差,
的协方差, 为
为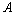 的转置矩阵。公式(5)(6)就是卡尔曼滤波器对系统的预测公式。
的转置矩阵。公式(5)(6)就是卡尔曼滤波器对系统的预测公式。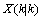 :
: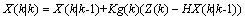 (7)
(7)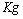 为卡尔曼增益:
为卡尔曼增益: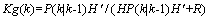 (8)
(8)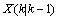 的协方差,实现Kalman滤波持续运行:
的协方差,实现Kalman滤波持续运行: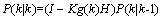 (9)
(9) 为1的矩阵。当系统进入k+1状态时,
为1的矩阵。当系统进入k+1状态时,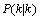 就是公式(6)的
就是公式(6)的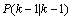 。
。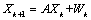 (10)
(10)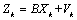 (11)
(11)